Recent trends V: The Weighted Region Problem

24 Jun 2024

Shortest path problems, where the goal is to find an optimal path between two points in the plane, are among the fundamental problems in computational geometry. These problems are crucial for a variety of applications, GPS navigation is perhaps the best-known application. However, there are numerous daily-life problems that can be solved using shortest path algorithms. For another well-known example, robot vacuum cleaners need to navigate through environments, avoiding obstacles and reaching a target location efficiently. Also, in the realm of video game development, creating realistic and challenging game worlds often involves pathfinding for non-player characters.

The most general version of the shortest path problem considers a subdivision of the two-dimensional plane into regions (see Figure 1), where each region $R_i$ has a weight $\omega_i \geq 0$ reflecting about how fast one can move inside that region (or how costly it is to do so).

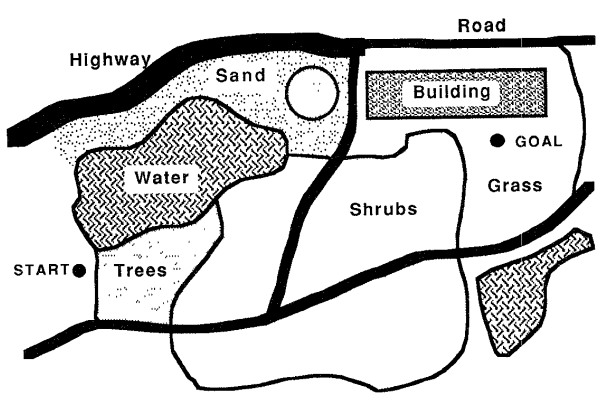
Back to the example of a robot vacuum cleaner, moving on a carpet is more costly than on a hard floor. In general applications, the moving object can have different speeds when traversing a road, a dirt track, a forest, or a swamp area. Furthermore, the speeds may also depend on other factors such as time of day, precipitation, or the location of other bodies.

The resulting metric is called the Weighted Region Metric, and the problem of computing a shortest path between two points under this metric is known as the Weighted Region Problem (WRP) (Mitchell and Papadimitrou 1991). In this setting, a straight-line segment $\sigma$, of Euclidean length $|\sigma|$, between two points in the same region has weighted length $\omega_i \cdot \rvert \sigma \lvert$ when traversing the interior of region $R_i$, or $\min{\omega_i,\omega_j} \cdot\rvert \sigma \lvert$ if it goes along a boundary shared by regions $R_i$ and $R_j$. Then, the weighted length of a path $\pi(s,t)$ through a subdivision, denoted by $\lVert \pi(s,t) \rVert$, is the sum of the weighted lengths of its subpaths through each face or edge. The WRP entails computing a weighted shortest path $\mathit{SP_w}(s,t)$ between two given points $s$ and $t$ under this metric.

It would be great if one could obtain a weighted shortest path exactly and using a reasonable amount of time and space, but this problem seems to be hard. In 2014, De Carufel et al. (De Carufel et al. 2014) proved that computing an exact shortest path between two points using the Weighted Region Metric—in its general formulation—is an unsolvable problem in the Algebraic Computation Model over the Rational Numbers ($\mathit{ACM\mathbb{Q}}$). In the $\mathit{ACM\mathbb{Q}}$ model, one can exactly compute any number that can be obtained from rational numbers by applying a finite number of operations from $+, -, \times, \div$, and $\sqrt[k]{}$, for any integer $k \geq 2$.

Therefore, in applications where the WRP arises, which usually require efficient and practical algorithms, several approximation algorithms have been proposed. The general idea of these algorithms is to discretize the geometric space. One such technique, developed by Mitchell and Papadimitriou in 1991 (Mitchell and Papadimitrou 1991), is based on the continuous Dijkstra’s algorithm, subdividing triangle edges in parts for which crossing shortest paths have the same combinatorial structure. Since the seminal work by Mitchell and Papadimitriou, several approximate solutions were proposed, with improvements on running times, and based on adding Steiner points on the boundary or inside the regions (e.g., see (Aleksandrov et al. 1998; Aleksandrov, Maheshwari, and Sack 2000, 2005; Bose, Esteban, and Maheshwari 2024; Sun and Reif 2006)). However, results on WRP typically keep some dependency on the vertex coordinates sizes and weight ranges.

Yet another technique consists on approximating the domain by using a (weighted) tessellation $\mathcal{T}$. See Figure 2.

Then, an approximation is considered by computing a shortest path on a weighted graph associated to $\mathcal{T}$. Convex polygons, and overlapping disks —of different sizes— are among the most frequently used region shapes. Nonetheless, regular meshes are the dominant and simplest shape representation scheme in computer graphics. In general, regular meshes are easy to implement, and are a natural choice for environments that are grid-based by design (e.g., many game designs). In addition, some search and optimization algorithms can be optimized for square (Ammar et al. 2016; Nagy 2003), or regular-hexagon grids (Björnsson et al. 2003).

Recently, Bose et al. (Bose et al. 2022a, 2022b, 2023), as part of the PhD thesis of Guillermo Esteban, studied how well a shortest path computed on a weighted regular mesh approximates the actual shortest path. In particular, comparing a shortest grid path $\mathit{SGP_w}(s,t)$ in the graph where every corner of the mesh is joined by an edge to a predefined set of $k$ neighbors, to the actual shortest path $\mathit{SP_w}(s,t)$. See Figure 3 for a comparison between the two types of shortest paths in a square tessellation.

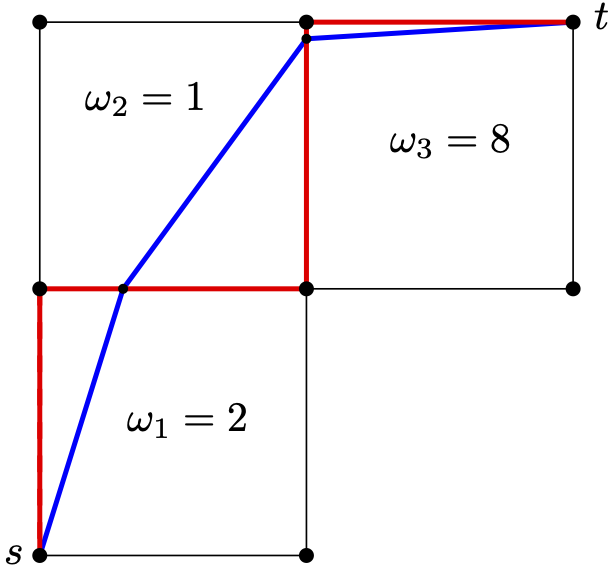
As main results on this research line, the mentioned thesis provided the following bounds for the ratio $\frac{\lVert \mathit{SGP_w}(s,t)\rVert}{\lVert \mathit{SP_w}(s,t)\rVert}$:
It is at most $\frac{2}{\sqrt{3}} \approx 1.15$, $\frac{2}{\sqrt{2+\sqrt{2}}} \approx 1.08$ and $\frac{2}{\sqrt{2+\sqrt{3}}} \approx 1.04$ in an equilateral-triangle, a square and a regular-hexagon mesh, respectively. These bounds provide a theoretical justification for practical applications using shortest paths computed on a regular mesh, since they guarantee approximation errors of at most $15\%$, $8\%$ or $4\%$, depending on the type of mesh used.

Finally, let us mention a very surprising and counter-intuitive finding: These worst-case upper bounds are independent of the particular assignment of weights to the regions in the tessellation. That is, the same bounds hold no matter whether some regions have a cost much higher than the others (independently of how many are they), or all the regions have the same cost (independently of how high this is).

References

1. Aleksandrov, L., M. Lanthier, A. Maheshwari, and J.-R. Sack. 1998. “An ϵ-Approximation Algorithm for Weighted Shortest Paths on Polyhedral Surfaces.” In Scandinavian Workshop on Algorithm Theory, 11–22. Springer.
2. Aleksandrov, L., A. Maheshwari, and J.-R. Sack. 2000. “Approximation Algorithms for Geometric Shortest Path Problems.” In Proceedings of the Thirty-Second Annual ACM Symposium on Theory of Computing, 286–95.
3. Aleksandrov, L., A. Maheshwari, and J.-R. Sack.. 2005. “Determining Approximate Shortest Paths on Weighted Polyhedral Surfaces.” Journal of the ACM 52 (1): 25–53.
4. Ammar, A., H. Bennaceur, I. Chǎari, A. Koubǎa, and M. Alajlan. 2016. “Relaxed Dijkstra and A^* with Linear Complexity for Robot Path Planning Problems in Large-Scale Grid Environments.” Soft Computing 20 (10): 4149–71.
5. Björnsson, Y., M. Enzenberger, R. Holte, J. Schaeffer, and P. Yap. 2003. “Comparison of Different Grid Abstractions for Pathfinding on Maps.” In IJCAI, 1511–12. Citeseer.
6. Bose, P., G. Esteban, and A. Maheshwari. 2024. “A Steiner-Point-Based Algorithm for Approximate Shortest Paths in Weighted Equilateral-Triangle Meshes.” Theoretical Computer Science, 114583.
7. Bose, P., G. Esteban, D. Orden, and R. I. Silveira. 2022a. “On Approximating Shortest Paths in Weighted Hexagonal Tessellations.” In Abstracts of the Computational Geometry: Young Researchers Forum 2022 (CG:YRF), 27–31.
8. Bose, P., G. Esteban, D. Orden, and R. I. Silveira. 2022b. “Spanning Ratio of Shortest Paths in Weighted Square Tessellations.” In Abstracts of the 38th European Workshop on Computational Geometry (EuroCG), 65:1–8.
9. Bose, P., G. Esteban, D. Orden, and R. I. Silveira. 2023. “On Approximating Shortest Paths in Weighted Triangular Tessellations.” Artificial Intelligence 318: 103898.
10. De Carufel, J.-L., C. Grimm, A. Maheshwari, M. Owen, and M. Smid. 2014. “A Note on the Unsolvability of the Weighted Region Shortest Path Problem.” Computational Geometry 47 (7): 724–27.
11. Mitchell, J. S. B., and C. Papadimitrou. 1991. “The Weighted Region Problem: Finding Shortest Paths Through a Weighted Planar Subdivision.” Journal of the ACM 38 (1): 18–73.
12. Nagy, B. N. 2003. “Shortest Paths in Triangular Grids with Neighbourhood Sequences.” Journal of Computing and Information Technology 11 (2): 111–22.
13. Sun, Z., and J. H. Reif. 2006. “On Finding Approximate Optimal Paths in Weighted Regions.” Journal of Algorithms 58 (1): 1–32.

---

The author of this post, Guillermo Esteban Pascual, is a doctoral researcher at the University of Alcalá.